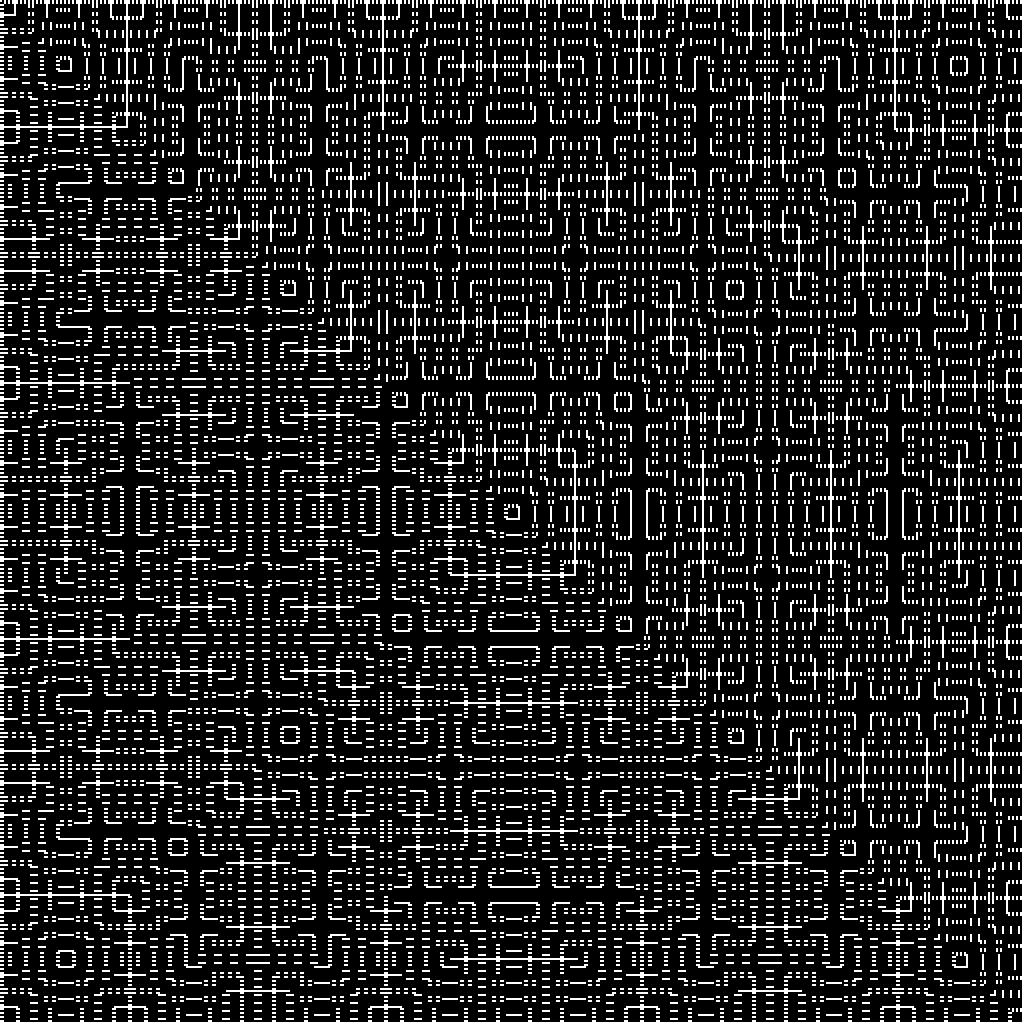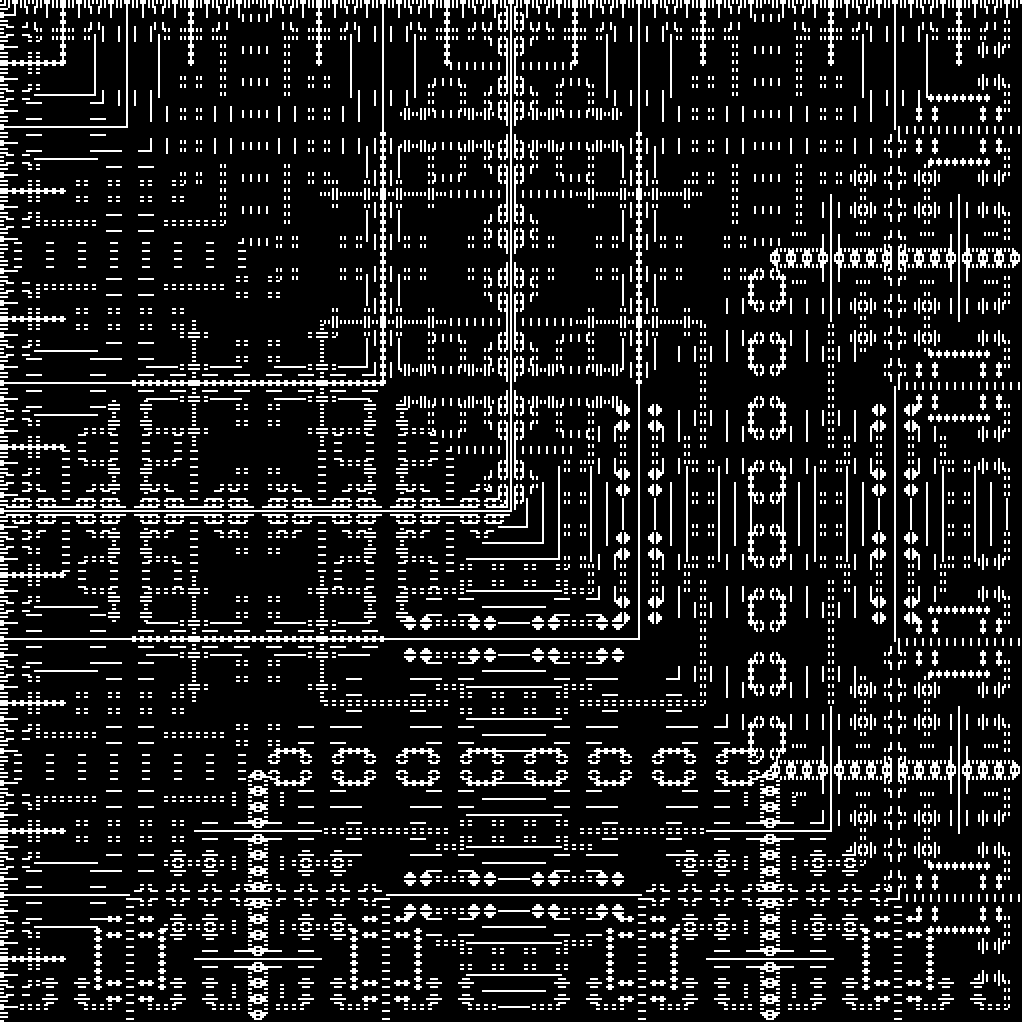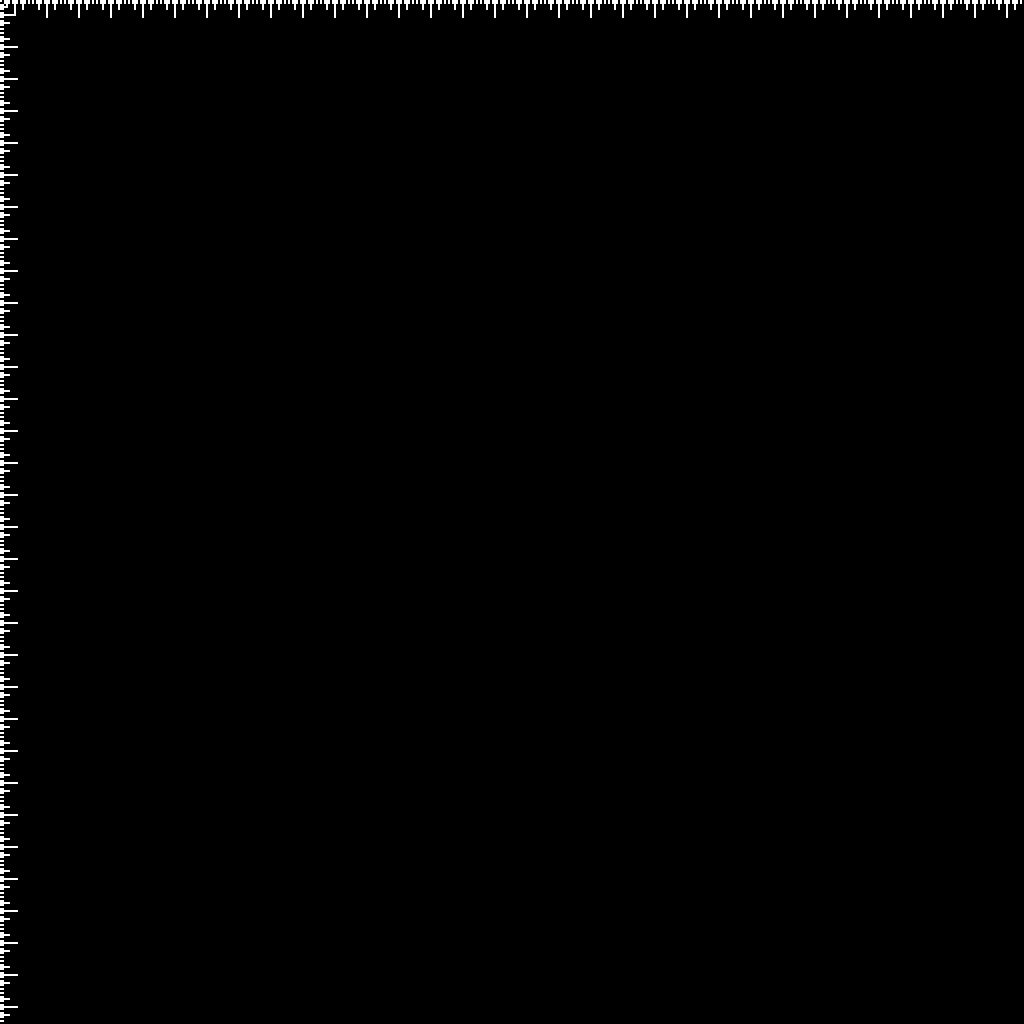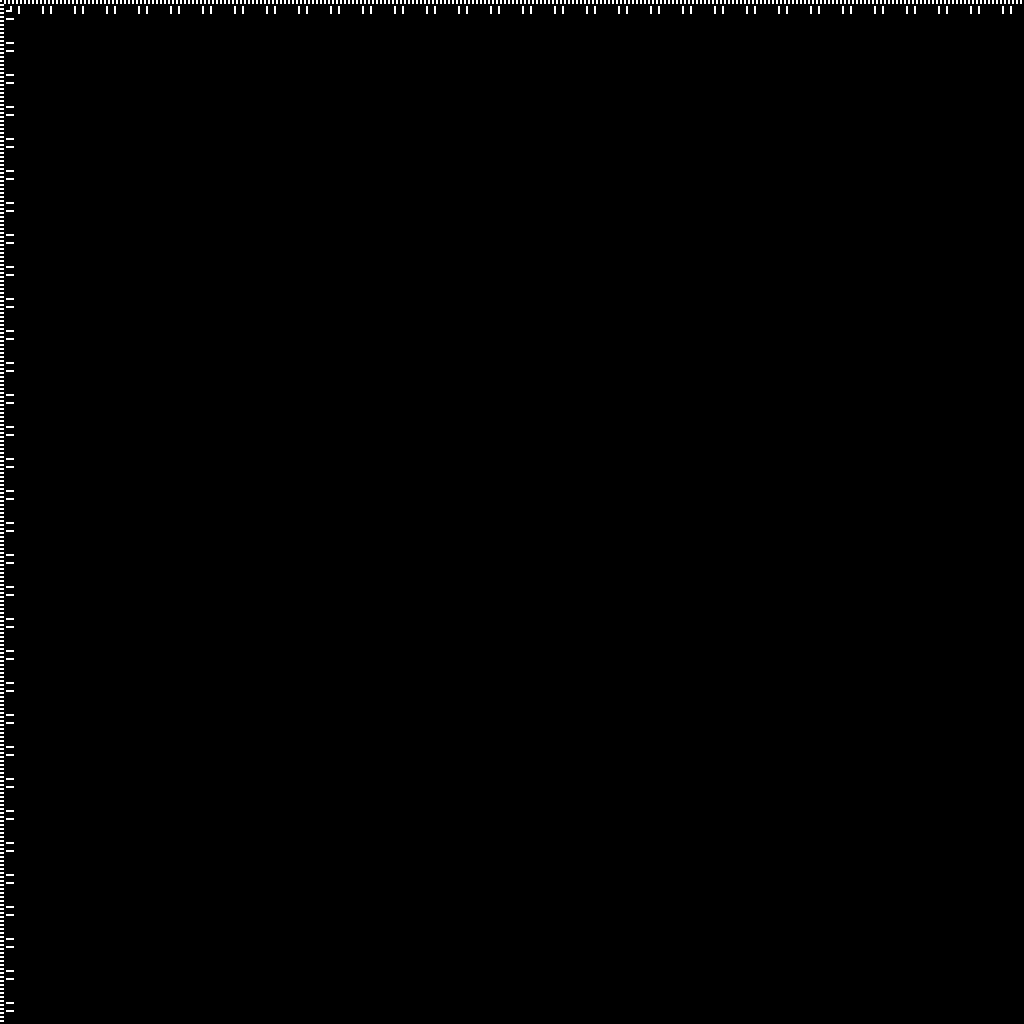Playing with Bit Fields
EPILEPSY WARNING
The Original: (x ^ y) % 9
While scrolling through Twitter, I found this one tweet by @aemkei that peaked my interest.
I'm fascinated by this simple formula to create bit fields that look like alien art:
— Martin Kleppe (@aemkei) April 2, 2021
(x ^ y) % 9 pic.twitter.com/jZL15xzEDL
The image immediately caught my attention, along with the formula $(x \otimes y) \mod 9$. In this case, this is a N-by-N image where each pixel x value and y value are used in a bitwise-XOR function, followed by performing a modulo operation with the number 9. Martin Kleppe, the author, would also show other examples with different using different modulo values than 9, showing how different yet similar these images can be.
More examples:
— Martin Kleppe (@aemkei) April 2, 2021
(x ^ y) % 5
(x ^ y) % 17
(x ^ y) % 33
(inspired by https://t.co/vw6rOrA3T9) pic.twitter.com/AnKVTTIbwS
After seeing this, and Foldster’s example, I was tempted to try out some of my own examples, and seeing that Martin was kind enough to post the source code in a separate tweet, I decided to try some examples out.
Playing with Modulo and Bitwise XOR
I started with Martin’s original example of $(x \otimes y) \mod 9$ to test the code and then tried some other, similar examples that he didn’t create.
| mod 10 | mod 11 |
|---|---|

|

|
We can see similarities between these two modulos with slight differences. We can expand this to make an animation of these modulos to see what we would expect.
Although the width and height are 1024px, they change 4 pixels at a time in a square, meaning there are 256x256 large pixels that we are dealing with. With this information, we can try modulo from 1 to 255.

What a nice transition!
Bitwise OR
If we use $(x \lor y) \mod N$, we can see some interesting patterns. Particularly, a form of Sierpinski’s Triangle can be seen at $(x \lor y) \mod 255$.

We can get a nice animation by going through the modulo of 1 to 255.

Extra Animations
Here are some other ones that I enjoyed. If you want to view the original source code, you can go to the original tweet.
However, my modified code that shows the animation is available on my Github. In these examples, the N is the value cycling through the animation.
Enjoy!
Bitshift
[N = 224, N <= 255, N + 1]
((x & y) >> N)

Combination of Multiplication and XOR
[N = 1, N <= 255, N + 1]
(((x * y) & N) & ((x ^ y) & N))

Foldster’s Bitfield
[N = 1, N <= 255, N + 2]
(((abs(x+y)^abs(x-y)+1)**N) % 7)